Optical phase estimation approaching the quantum limit in a single shot.

December 3, 2020

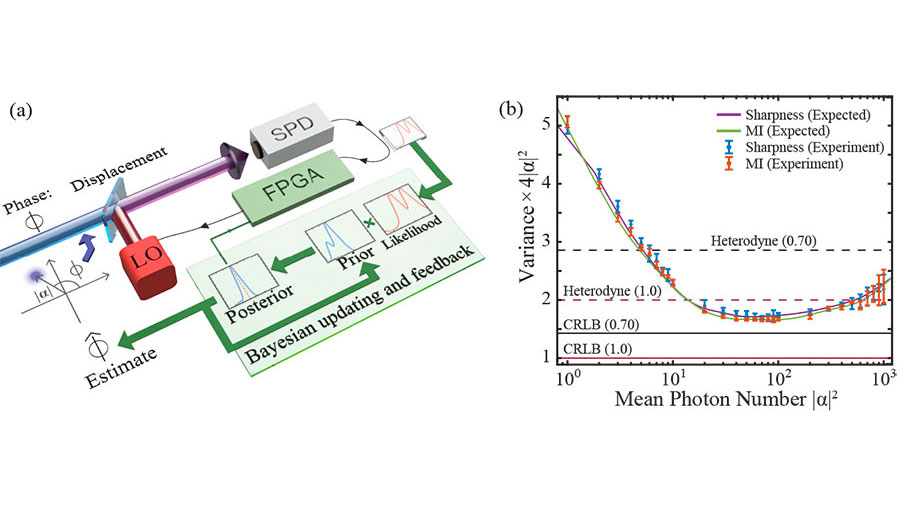
Optical phase estimation figure for article
(a) The input state and optimized local oscillator (LO) interfere on a beam splitter such that the input is displaced in phase space. The probability distribution for the unknown phase is then updated according to Bayes rule and new optimal values for the LO are applied. (b) Experimental data (points with error bars) shows that adaptive non-Gaussian measurements surpass the limits of ideal heterodyne detection (dashed red) and approach the fundamental sensitivity limit given by the CRLB for our detection efficiency of 70% (solid black)

Optical phase estimation is at the center of many metrological tasks where the value of a physical parameter of a system is mapped to the phase of an electromagnetic field, and single-shot measurements of this phase retrieve the information of this parameter. In this article, we demonstrate optimized estimation strategies for single-shot measurements for the optical phase of coherent states, which achieve sensitivities surpassing the heterodyne limit and potentially approaching the quantum limit, the Cramer-Rao lower bound (CRLB). These strategies are based on optimized photon counting, coherent displacement operations, and fast feedback. Our demonstration uses fast processing for optimizing the single-shot measurement during the optical mode, and enables surpassing the heterodyne limit for a wide range of optical powers without correcting for detection efficiency of our system. This is, to our knowledge, the most sensitive single-shot measurement of an unknown phase encoded in optical coherent states.

Read more at the American Physical Society (APS).