Research
Quantum Computation
Quantum computation utilizes the counterintuitive behavior of quantum mechanics to achieve a speedup in computational power. Instead of the traditional bit values (0's and 1's) of digital computers, a quantum computer utilizes superpositions of these values, allowing it to occupy multiple different computational states at once. Quantum computers use this "quantum parallelism" to perform such computational tasks as searching large databases, designing new medical drugs, and deciphering cryptographic codes at a speed unmatched by ordinary digital computers.
Despite the phenomenal progress of the last two decades, much work remains before a realistic quantum computer can be built. Scaling up our current experimental setups to larger sizes is a major challenge. The superpositions which give quantum computers their characteristic power are fragile to interactions with the surrounding environment. A great deal of effort has been spent developing scalable hardware and control schemes which isolate quantum computers from these effects. Clever theoretical innovations, such as effective usage of many-body phenomena and methods of quantum error correction, also hold great promise for unlocking the tremendous potential of quantum computation, leading many researchers to believe that quantum computers will become an everyday reality in the not-too-distant future.
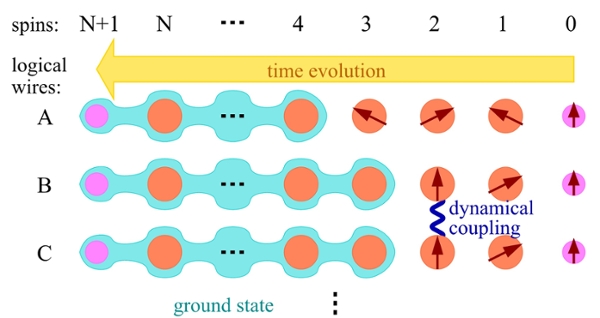
Many-body Physics
Many-body physics is the study of systems composed of many interacting particles. While the problems of many-body physics - especially those pertaining to quantum systems - have historically been regarded as difficult to solve, the development of new theoretical tools in the last thirty years has led to an explosion in our understanding of the general behavior of many-body systems. This has in turn contributed to the discovery and characterization of entirely new many-body phenomena, such as exotic "quantum phases" of matter, whose very existence relies upon the laws of quantum mechanics.
Increasingly, researchers in different areas of physics have realized that strong connections exist between quantum many-body physics and the study of quantum computation. On one hand, quantum computers, themselves being large interacting quantum systems, hold great promise for analyzing the behavior of those many-body systems which have traditionally resisted analysis. On the other, several varieties of quantum many-body systems have been shown to be excellent architectures for quantum computation. Because many commonly-studied quantum many-body systems occur in nature, a means of carrying out quantum computation with such systems would allow nature to do much of the work in constructing a quantum computer, putting us in a good position for achieving practically useful quantum computation.
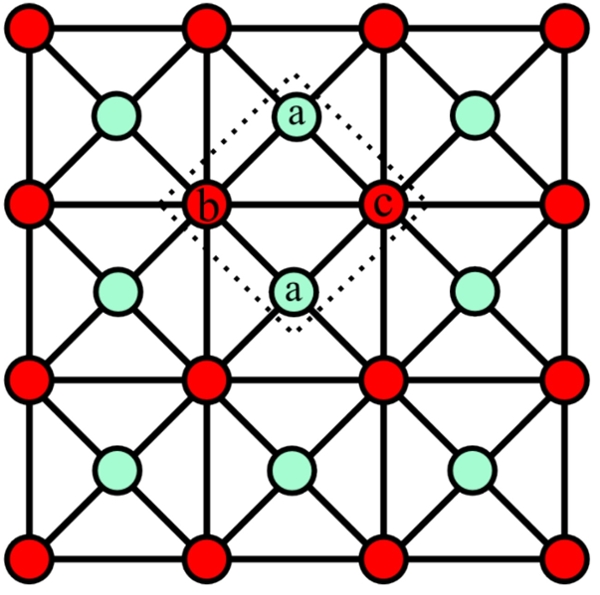
Near-term quantum algorithm for physics and chemistry
The most promising of quantum algorithms offer dramatic speed-ups compared to their classical counterparts; however, they require large-scale, error-corrected quantum computers in order to be implemented. Current quantum technologies are not yet at this stage, but rather have been dubbed as “noisy intermediate-scale quantum” (NISQ) computers. This descriptor refers to the fact that their computational power is limited by sensitivities to noise, yet their size already begins to surpass the capabilities of even the largest of supercomputing clusters. Exploring the limits of these NISQ computers is therefore of great importance to the continued progress of quantum computation.
One of the most interesting applications of quantum computation is the simulation of interacting electrons, such as in quantum chemistry and superconducting materials. While this is a challenging problem to scale-up with classical computation, it is a natural task for a quantum computer. In the context of NISQ computers, one must tailor the simulation algorithms for their hardware limitations, and thus novel techniques must be developed in order to utilize their unique computational power. In particular, co-designing these algorithmic techniques with a real device is essential for the practical implementation of such algorithms.
Entanglement and contextuality for quantum advantage
One fundamental way that quantum bits differ from the classical bits stored in your laptop are the types of questions we can ask about them. While simply looking at a classical bit can reveal it to be a 0 or 1, quantum bits can be measured in a variety of ways, since possibilities 0 and 1 may exist in superposition. However, quantum mechanics forbids us from learning too much information about our qubits at once, and we are forced to be selective about which questions we ask.
Since the early days, physicists have been perplexed and intrigued by the “spooky action at a distance,” characteristic of measurements performed on spatially separate parts of an entangled quantum state. Today we understand more generally that much like how the meaning of a word in a sentence can depend on the context in which it appears, the outcome of a quantum measurement can depend on other measurements independently performed with it. This nonclassical phenomenon is aptly called “quantum contextuality,” and has been identified as one of fundamental resources that gives a quantum computer its power. We explore the utility of contextuality in quantum algorithms and the foundational role it plays in quantum computation.

Quantum Simulation
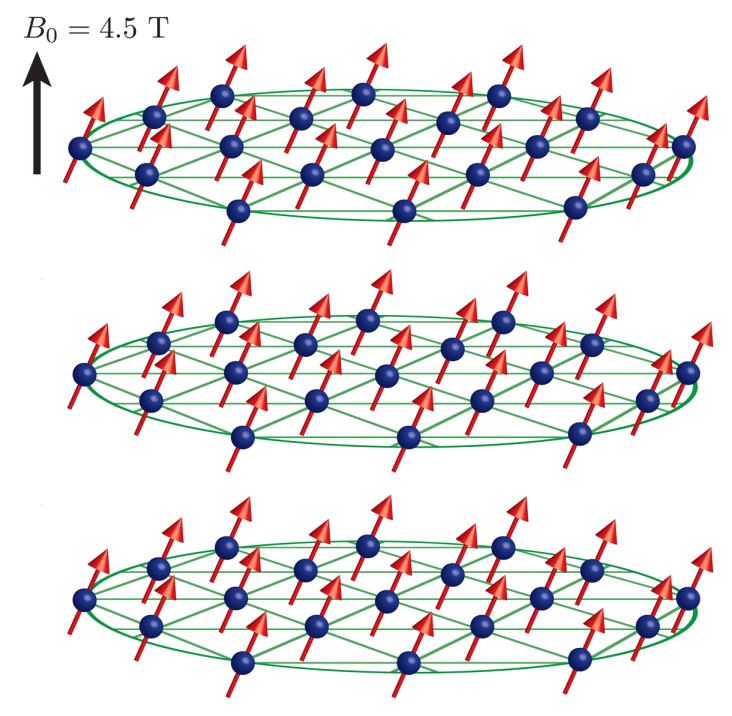
When quantum computing comes to the fore, its "killer app" will likely be the ability of quantum computers to simulate other quantum systems. As quantum effects are ubiquitous in nature, universal quantum simulation would have applications in quantum physics, quantum chemistry, biology, and even such areas of classical physics as cosmology, making it an attractive goal. It was this prospect that originally motivated Feynman to propose the idea of performing computation with quantum systems in the early eighties. A generic quantum state naively requires exponentially many complex amplitudes to describe it, and so a classical computer cannot even store the description of such a state efficiently, let alone simulate its evolution in time. This exponential tractability gap is only bridged when one considers simulating a quantum system on a computer composed of quantum elements.
Is universal quantum computation truly necessary for this purpose? Today, many researchers are turning to the analog construction of quantum simulators. These devices are not universal but specifically tailored to mimic a small variety of other quantum systems. Progress in this direction has come in the form of ion traps, atoms and molecules trapped in optical lattices, superconducting qubits, and so on. However, many challenges remain as well, the foremost being scaling these systems up in the face of error propagation. As the complexity of encoded information grows, so does that of its errors. It is therefore important to address the question of whether or not quantum simulators are feasible without relying on established quantum error correction techniques. Consequently, the challenge of quantum simulation unifies many seemingly-disparate subfields of quantum computation and is a powerful driving force behind the field today.
 The National Science Foundation supports CQuIC under
The National Science Foundation supports CQuIC under 

