Research
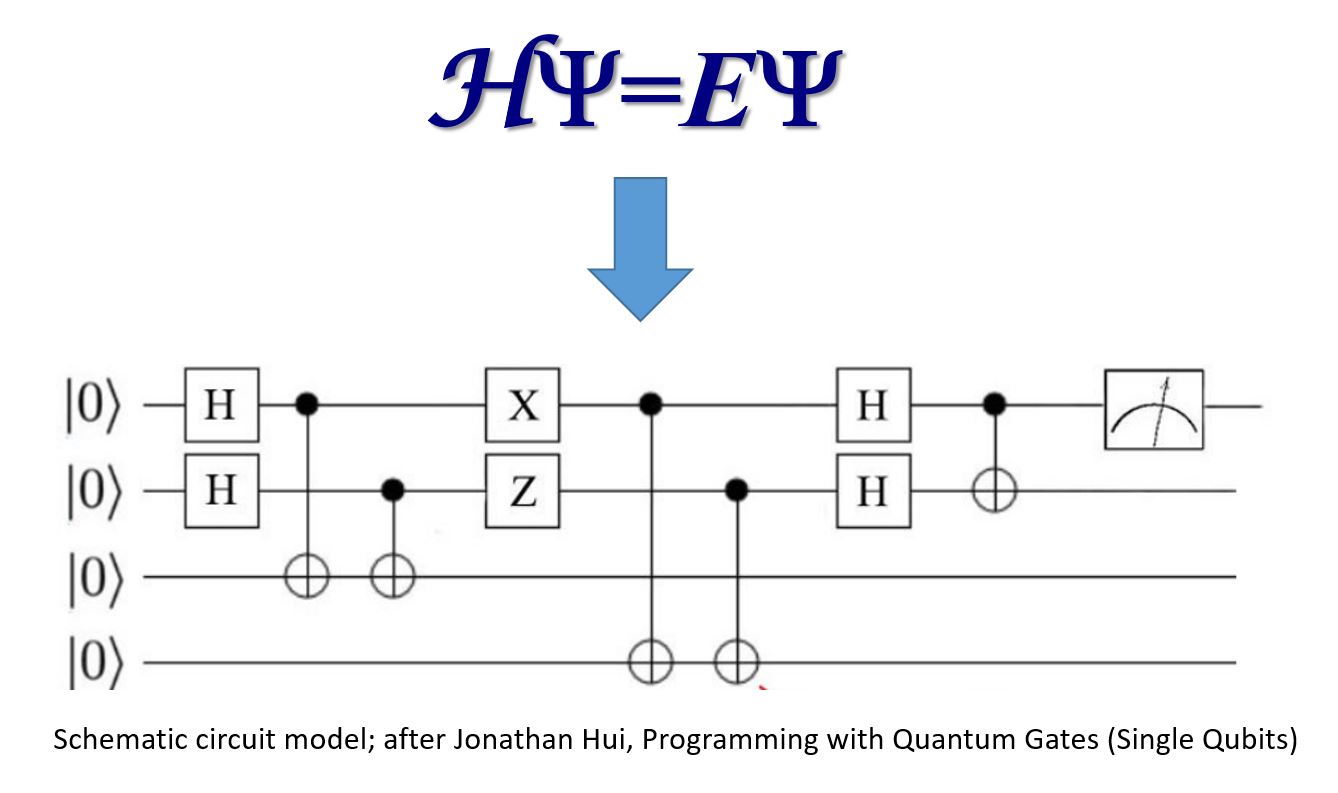
Quantum computing and the electronic structure problem
One of the most exciting potential applications of quantum computing is the electronic structure problem: finding the solution to the Schrödinger equation for many-electron systems such as molecules and periodic solids. As Feynman famously observed in his 1982 paper proposing quantum computers as universal quantum simulators, “nature is not classical”, and one might therefore hope to identify a natural and efficient quantum mapping of the electronic structure problem onto a quantum computer, to significantly accelerate time to solution for complex systems. Currently, most quantum computing architectures employ a quantum version of the classical Boolean logic circuit model, with quantum bits (qubits) as the computational elements, acted upon by a series of quantum logic gates. Within the constraints of this quantum circuit model framework, our research is aimed at exploring whether it is possible to construct fast, scalable, and accurate quantum electronic structure algorithms capable of exceeding the performance of existing quantum chemistry codes executing on traditional (classical) supercomputers.
Correlated electron density encodings
The quantum many-body wavefunction Ψ for a system of N electrons is a complex, simultaneous function of 3 N spatial coordinates. The complexity derives from the entanglement of electronic motion through quantum statistical correlations (due to the Pauli exclusion principle), and spatial correlations mediated by Ψ. These dual correlations place implicit constraints on the form of the wavefunction, and can be used to advantage in variational quantum chemistry methods for solving the time-independent Schrödinger equation. Starting from a suitably-constructed ansatz for Ψ, the expectation value of the total energy is minimized via iterative updates to the wavefunction. Currently, many researchers are exploring methods for efficiently implementing this approach on circuit model-based quantum computers.
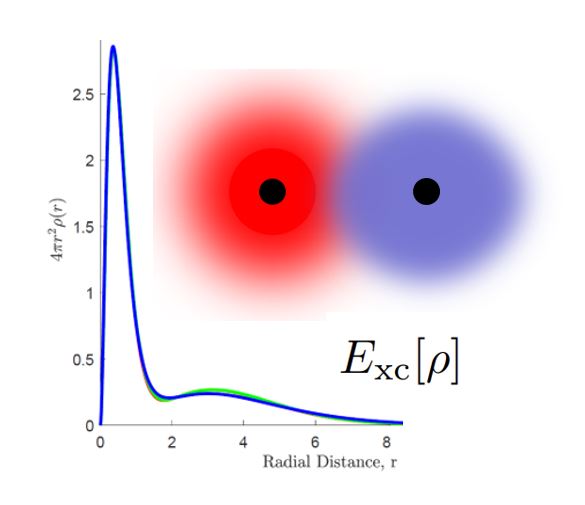
An alternative approach being explored in our group is based on the density functional theory (DFT) formulation of the electronic structure problem due to Hohenberg and Kohn (1964). DFT formally replaces the solution of the Schrödinger equation for Ψ, a function of 3 N coordinates, with a minimization problem for the total energy expressed in terms of the electron density ρ, a function of just three spatial coordinates. In practice, ρ is determined through the solution of a set of coupled, self-consistent set of single-particle equations (Kohn and Sham, 1965). The key innovation of DFT is that it formally folds the quantum complexity of the correlated wavefunction into a universal but unknown exchange-correlation functional. This functional must be approximated in practice. We are investigating methods for computing the DFT electron correlation energy in terms of entangled open system electron densities, and for efficiently mapping the resulting methodology onto quantum computing architectures. By ‘repackaging’ the electronic structure problem in terms of single-particle density constructs, we hope to achieve improved accuracy, convergence, and scaling for large quantum systems.
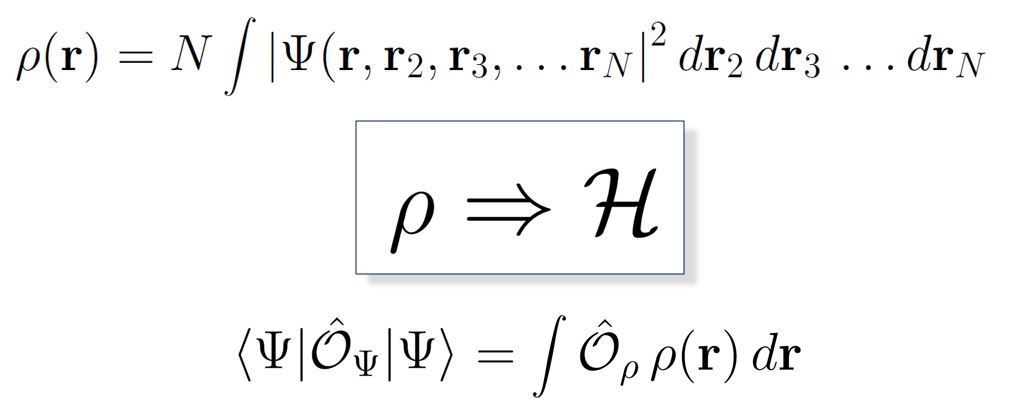
Noise-resilient algorithms for NISQ architectures
A related project is aimed at determining whether the DFT formulation of the electronic structure problem can be more resilient to noise on current-generation NISQ (noisy intermediate-scale quantum) computers, as compared to traditional quantum chemistry (wavefunction-based) electronic structure methods. Quantum computations of total energies for small molecule systems are being compared for diverse chemistry- and physics-based models of the exchange-correlation energy, vs. quantum chemical (wavefunction) methods. Different quantum computing architectures will be tested, to explore the effects of distinct physical qubit instantiations and topologies on molecular potential energy curves.
 The National Science Foundation supports CQuIC under
The National Science Foundation supports CQuIC under 

