November 21, 2024 - Alex Fischer

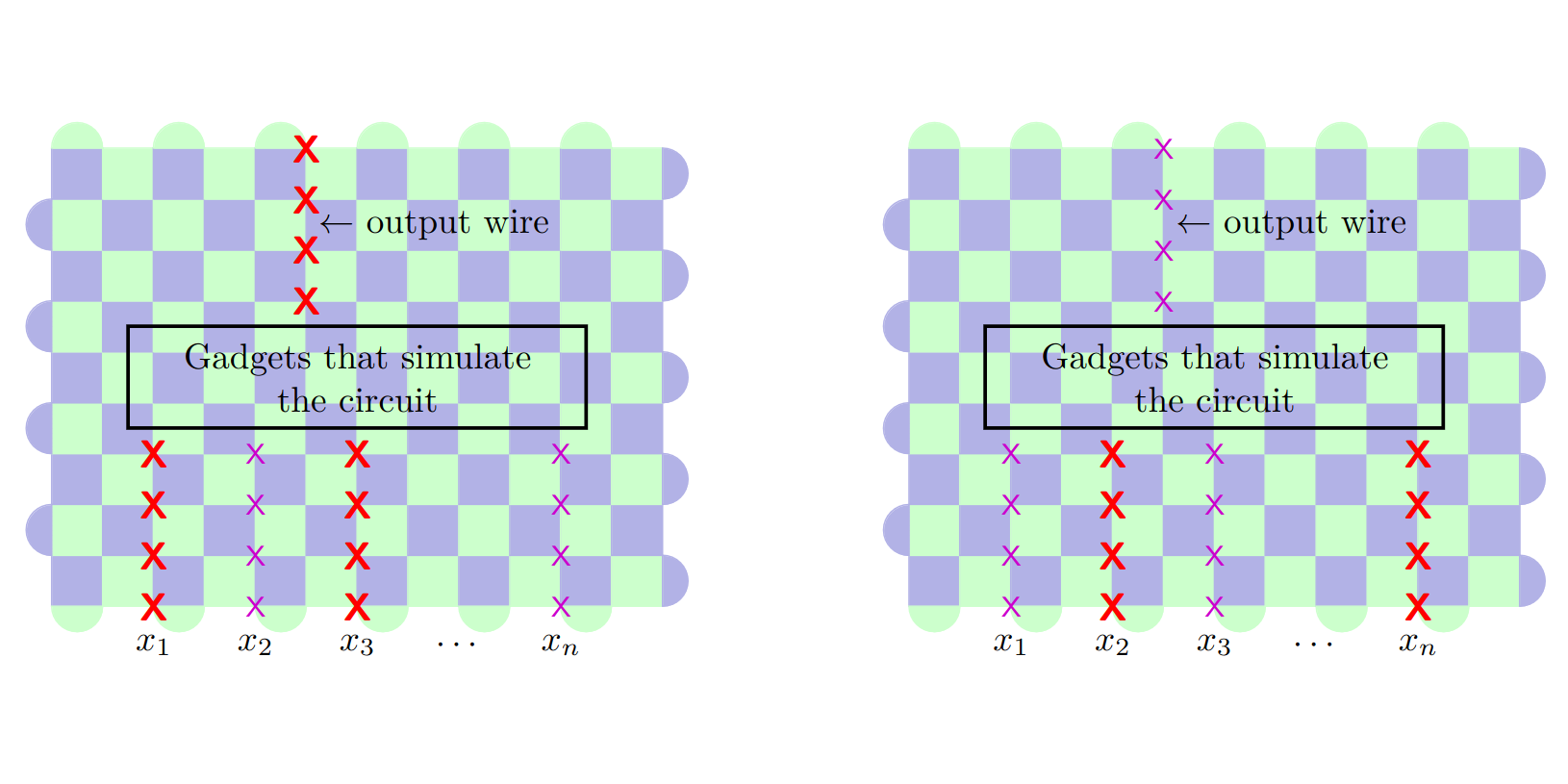Quantum computers are highly vulnerable to disturbances from their interactions with the external environment outside the computer. In order to do accurate quantum computation using quantum computers with these vulnerabilities, we have to store and process information in a redundant, failure-tolerant manner. Quantum error correcting codes are methods to store information in this manner. The surface code is one example of a quantum error correcting code that is highly promising due to its low demands on quantum hardware. Decoding is a computational problem that is necessary for quantum error correction: it is the problem of determining how to correct errors in the stored quantum information, given measurement results extracted from the quantum error correcting code. This decoding problem for the surface code is a widely studied problem, because the surface code is so promising and because decoding is a necessary problem to solve to use any such code.

Our work shows that various different formulations of the decoding problem for the surface code are computationally hard, in a rigorous sense. We do this by showing that surface code decoding problems can express other computationally hard problems. Our results require that the decoding problem be formulated such that the input to the problem includes a fine-grained description of possible errors that can occur. The practical impact of our work is not to discourage surface code use, but to show that practically useful decoding algorithms for the surface code cannot hope to solve the problem when the problem includes this fine-grained description of possible errors, else the problem would be too computationally hard. It tells us that we should focus research efforts for these algorithms on simpler cases that are not provably hard.

Read the paper at https://quantum-journal.org/papers/q-2024-10-28-1511/