Phase-Space Geometry and Optimal State Preparation in Quantum Metrology with Collective Spins
May 3, 2023 - Pablo Poggi
Quantum metrology establishes fundamental limits to the precision of estimating an unknown parameter encoded in a systems’ observable property, like the precession rate of a collection of spins in a uniform magnetic field. Most quantum metrology protocols rely on the preparation of a nonclassical entangled state, which serves as a sensing probe. Identifying the physical mechanisms that allow fast preparation of these probed entangled states and developing strategies to do so is of utmost importance for the design of reliable quantum sensing strategies.
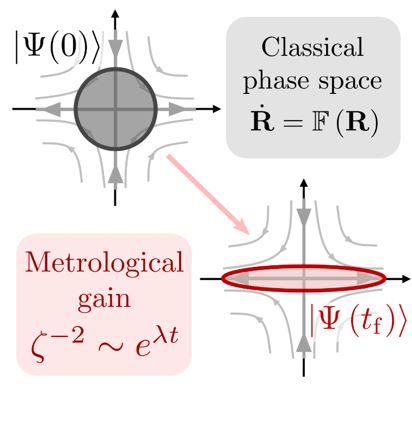
Recent work from CQuIC, led by former graduate student Manuel Muñoz-Arias (currently a postdoc at the Instititut Quantique in Sherbrooke) together with Regents’ Professor Ivan Deutsch and Research Professor Pablo Poggi, presents a simple framework that explains such physical mechanisms for a wide class of quantum systems. The team has achieved this by analyzing the state preparation procedure from a geometrical perspective. In this picture, the properties of the classical phase space associated with the collective degree of freedom of a system of many spin-1/2 particles dictates whether exponentially fast entanglement generation is in principle possible or not. If it is, the framework allows one to characterize the optimality of the state preparation as a function of system parameters, and to analytically obtain the timescale required to achieve the desired states.
This work, carried out with support of Q-SEnSE, an NSF Quantum Leap Challenge Institute, provides a unifying picture for many known quantum sensing protocols and explains their optimality (or lack thereof), and provides the tools to assess the performance of new strategies. More generally, the study elucidates general connections between quantum sensing and nonequilibrium phenomena in many-body physics such as dynamical phase transitions. The results are published in the journal PRX Quantum and can be accessed online [1].
[1] Manuel H. Muñoz-Arias, Ivan H. Deutsch, and Pablo M. Poggi, Phase-Space Geometry and Optimal State Preparation in Quantum Metrology with Collective Spins, PRX Quantum 4, 020314 (2023).
