Effect on Chaos on the Simulation of Quantum Critical Phenomena in Analog Quantum Simulators
December 15, 2021 - K. Chinni, P. Poggi and I. Deutsch
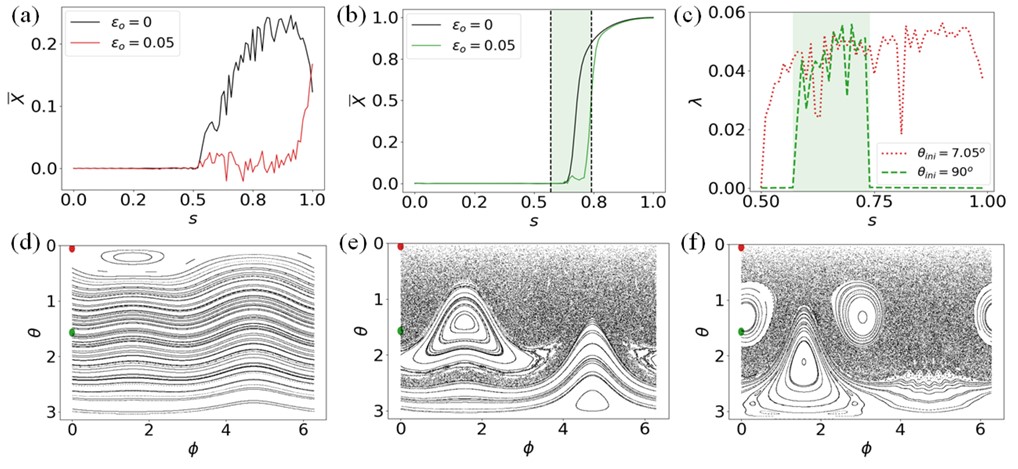
The ideal and the perturbed bifurcation plots associated with (a) the GSQPT and (b) the DQPT are shown by the black and the (a) red and (b) green colored curves, respectively, as a function of the control parameter, s. (c) Lyapunov exponents are plotted as a function of s for initial conditions corresponding to GSQPT (dotted line) and DQPT (dashed line). (d-f) Poincaré sections in the presence of chaotic perturbation are shown here for different values of the control parameter as a function of the coordinates of the classical phase space, 𝜃 and 𝜙.
Since Feynman's proposal of quantum simulation, rapid advancements in the field have brought us into the current era of Noisy Intermediate-Scale Quantum (NISQ) devices. These devices are large enough such that, absent noise, they may be able to tackle problems that are intractable for classical computers. However, their size and noise levels are still far from the requirements of quantum error correction techniques. Hence, it is not fully understood if we can trust simulation performed on these devices. Of particular interest is the simulation of quantum phase transitions. Generically, systems have the most complexity near the critical point, and thus are expected to be most sensitive to imperfections near that point. In a recent work published in Physical Review Research [1], a CQuIC team led by graduate student Karthik Chinni, along with CQuIC faculty Pablo Poggi and Ivan Deutsch, tackled this problem by studying a mean-field model where quantum phase transitions can be described motion in a classical phase space. A continuous phase transition occurs we a fixed point bifurcates going from stable to unstable. This is the point that first becomes chaotic whenever the system is subject to a non-integrable perturbation. In this work, they explore the effects of chaos on the quantum simulation of various aspects of the ground-state quantum phase transition (GSQPT) and dynamical quantum phase transition (DQPT) present in the Lipkin-Meshkov-Glick model, which is an integrable system, in the presence of an oscillating background field that makes the system chaotic.
More specifically, they have proposed a protocol inspired by the classical dynamics (thermodynamic limit) for extracting critical points of both the GSQPT and the DQPT. Using this, they study how the chaos arises in the LMG model in the presence of a nonintegrable perturbation. They show that the time-averaged magnetization, which is the output of the dynamical quantum simulator considered here, becomes sensitive at the parameter values in the Hamiltonian when the associated initial condition is located in chaotic region of the classical phase space. However, the critical point estimates remain robust as they signal a global change in the structure of the phase space, which occurs even in the presence of perturbation as the system becomes chaotic around this point. These results indicate that the dynamical complexity can have fundamental effects on the reliability of quantum simulation.
