Quantum and Classical Nonlinear Dynamics of p-spin Kicked Tops
May 19, 2021 - Manuel Muñoz-Arias, in collaboration, Pablo Poggi and Ivan Deutsch
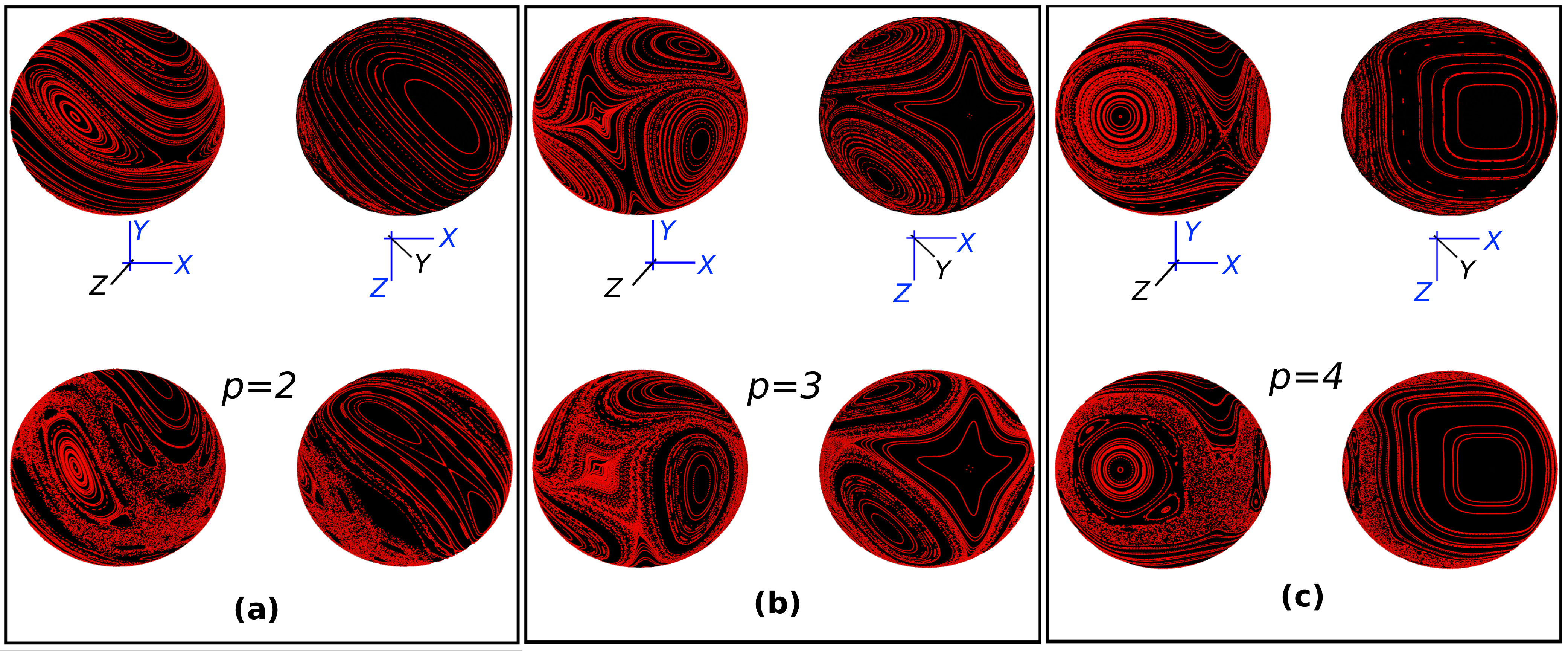
Figures (a), (b) and (c) show phase portraits for the first three kicked p-spins, with p = 2, 3, 4. Top and bottom rows show the phase portraits for two different values of the kicking strength, giving fully regular dynamics and a mixed phase space, respectively.
Studying quantum chaos in strongly-correlated many-body systems is key to understanding quantum complexity and its implications for statistical physics, phases of matter, nonequilibrium dynamics, and information processing. As the general description of such phenomena represents a grand challenge for Quantum Information Science (QIS), it is useful to study toy models that elucidate essential features and phenomenology. To that end, the Kicked Top, introduced in 1987 by Fritz Haake and collaborators [1], was seminal in deepening our understanding of quantum chaos, and more recently its relationship to quantum simulations of quantum phase transitions. It describes a large spin-J that precesses around a fixed axis and is periodically kicked by quadratic twisting term. It is also a Trotter approximation to a traverse Ising model with all-to-all two-body pairwise interactions.
A team led by PhD student Manuel Muñoz-Arias, in collaboration with Pablo Poggi and Ivan Deutsch, has recently generalized this to so called p-spin models, a traverse Ising model with all-to-all p-body interactions; the Kicked Top is a special case with p=2. In a new publication in Physical Review E, Muñoz et al. presented the full characterization of the classical and quantum chaos of the family kicked p-spin models [2]. The rich nonlinear dynamics of this family shows surprising new features with potential implications for quantum simulation of quantum critical phenomena.
In this work, Muñoz et al. study both the quantum Floquet map and its classical (thermodynamic) limit. They show that regardless of the order of the interaction p, classically all models transition to global chaos in the same way. However, for weak kicking strengths, the models with p>2 display richer phenomena, with higher order bifurcations that introduce a type of complexity that is absent in the p=2 Kicked Top. These signatures of chaos persist into the quantum regime, as characterized in kinematic and dynamics properties. This new quantum complexity will have direct consequences when kicked p-spin models are used to describe gated-based quantum simulators and sensors.
[1] Haake, Kuś, and Scharf, Z. Phys. B 65, 381 (1987)
[2] Manuel H. Muñoz-Arias, Pablo Poggi, and Ivan Deustch, “Nonlinear dynamics and quantum chaos of a family of kicked p-spin models”, Phys. Rev. E 103, 052212 (2021)
