Quantum Computation from Symmetric Quantum Matter
December 6, 2016 - Jacob Miller
Jacob Miller and Akimasa Miyake have recently published a paper in Nature Partner Journal Quantum Information showing that quantum computers with distinct operational advantages can be built using a form of symmetric topological matter. Their work deals with measurement-based quantum computation (MQC), a way of powering computation with only single-spin measurements and a large entangled quantum “resource” state. MQC is a natural way to study the connection between different forms of quantum topological order, the types of quantum computation they can power, and what measurements are needed for this computation.
The authors show that two complementary forms of symmetric topological order are particularly useful for quantum computation. While previous resource states have only utilized the first form, a new Union Jack state is constructed to study the second, stronger form. While both are sufficient to achieve any desired computation, the quantum order found in the Union Jack state can achieve this using simpler measurements, pointing towards a surprising new resource for simplifying quantum computation.
The full article is available online at http://www.nature.com/articles/npjqi201636.
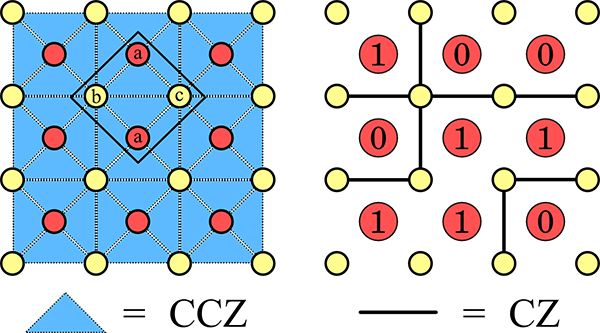
(Left) The Union Jack state, a new state with a strong form of symmetric quantum order which makes it useful for quantum computation. (Right) One step in the procedure for computing with the Union Jack state. Measurements on half of the sites drive the system through a quantum phase transition, which leads to a computationally useful graph state being randomly condensed on the unmeasured spins.
