Doing More with Quantum Phases of Spin Chains
October 13, 2015 - Jacob Miller
Jacob Miller and Akimasa Miyake have recently published a paper in Physical Review Letters showing that a particular class of one-dimensional spin chains, belonging to a type of quantum phase, are uniformly useful for certain quantum information processing tasks. Our work takes place in the context of measurement-based quantum computation, a means of using entangled many-body systems to perform quantum computation requiring only measurements on individual spins. One advantage of this formalism is that it lets us make interesting connections between quantum information science, which deals with concepts like entanglement and quantum computation, and condensed matter physics, which is concerned with emergent phenomena and phases of matter.
Our result is that a particular phase of one-dimensional spin chains -- known as a symmetry-protected topological phase -- can be used to perform any single-qubit information processing task we would like. In particular, while standard measurement-based protocols require knowledge of all of the microscopic details of the many-body systems being worked with, our protocol works for any arbitrary state in this phase (so long as two minimal conditions on the state are met). Since 1D spin chains are limited to single-qubit operations in measurement-based quantum computation, this can be thought of as the best resource characterization we could hope for in a 1D symmetry-protected topological phase.
The full article is available online at http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.114.120506.
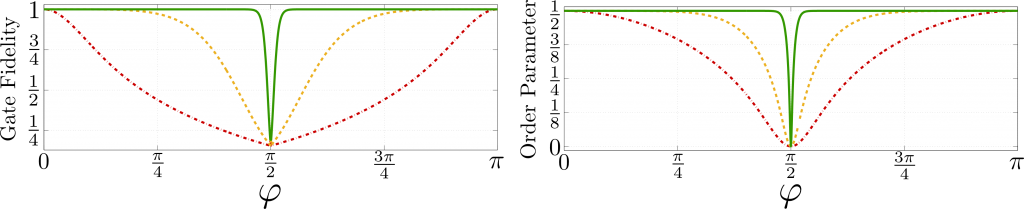
The close relationship between gate fidelity and a string order parameter for a class of states within our phase. Gate fidelity here quantifies how useful a state is for quantum information processing, while string order parameters are standard quantities used to characterize symmetry-protected topological phases. Our protocol works by first purifying arbitrary states into a "fixed-point" form, with the different curves here representing different degrees of purification. As the purification increases (red → yellow → green), the gate fidelity and string order parameter behave identically, demonstrating the close relationship between the quantum information and condensed matter aspects of this phase.
